IBM zur Rettung

10. Jul. 2017

Unser Forschungslabor verwendet eine große Vielfalt an Programmier- und Skriptsprachen, um Simulationen durchzuführen, Daten zu gewinnen, Ergebnisse zu analysieren und optimierte Lösungen zu finden. Die zwei Sprachen, die mir zur Zeit am besten gefallen, sind MATLAB und Python. Beide Sprachen sind einfach zu erlernen, anzuwenden, und verfügen über leistungsstarke Toolboxen und Module, die die Grundfunktionen von MATLAB bzw. Python erweitern. Dennoch wählen wir für die meisten Erstimplementierungen häufig MATLAB statt Python aus; vor allem weil es eine (aus meiner Sicht) sauberere Herangehensweise für große Matrixmanipulationen und komplexe Optimierungsaufgaben bietet. Sobald wir das Problem auf theoretischer Ebene gelöst haben, gehen wir zur zweiten Stufe über, wo Python die Berechnung beschleunigt (besonders wenn wir es auf unserem Rechencluster HTCondor einsetzen).

Doch mit dem jüngsten Problem, das wir angehen mussten, war der Übergang von Schritt eins zu Schritt zwei nicht einfach. Wir mussten sicherstellen, dass alle Komponenten korrekt funktionieren und unser Solver eine Lösung finden konnte. Doch mit zunehmender Anzahl von Eingabeparametern nahm das entwickelte Verfahren immer mehr Zeit in Anspruch. Tatsächlich war die Zeiterhöhung exponentiell, wenn die Anzahl der Parameter linear anstieg - nicht gut. Also, was könnten wir jetzt tun?

Fristen kamen auf uns zu und wir mussten mehrwöchige Probleme lösen, aber eine Lösung konnte erst nach einigen Tagen Rechenzeit ausgegeben werden. In diesem hoffnungslosen Moment schlug eine meiner Kolleginnen ein erstaunliches Tool namens CPLEX von IBM vor; sie hat uns wirklich das Leben gerettet, weil es für Akademiker kostenlos ist und um einiges schneller arbeitet als MATLAB (hier erhältlich). Wenn jemand also an dem mathematischen Problem interessiert ist, das wir lösen mussten und wissen mag warum es so schwierig ist, wie CPLEX im Vergleich zu native MATLAB Solvern funktioniert (und sich schlägt) und wie man CIPLEX erwirbt und in einem MATLAB Programm verwendet, dann ist dies der richtige Beitrag.

Das zu lösende Problem

In der Welt des Ressourcenverwaltung für Strom und Energienetze müssen Stromerzeuger vorausplanen, damit sie ihre Generatoren bei Bedarf einsetzen können. Dies geschieht in der Regel mit Hilfe einer Prognose, die jedoch bis zu einem gewissen Grad ungenau ist. Deshalb geben die Stromerzeuger nicht an, wie viel Energie sie liefern werden, sondern ob ihre Einheiten während einer bestimmten Zeit aktiv oder "eingesetzt" sind. Immer wenn Einheiten eingesetzt werden, können sie jede Menge Energie innerhalb ihrer Betriebsgrenzen bereitstellen, und die Betreiber können für diese Betriebszeiten planen, indem sie sicherstellen, dass genügend Ressourcen zur Verfügung stehen. Würde beispielsweise ein Wasserkraftwerk in der Zukunft für einige Stunden in Betrieb genommen, könnte der Betreiber sicherstellen, dass sich genügend Wasser in seinem Wasserreservoir befindet, so dass die Ressource ausreicht.

Da mehrere Generatoren mit unterschiedlichen Kosten und Emissionswerten arbeiten, musste ein Lösungsansatz gefunden werden, um dieses komplexe "Unit Commitment" (UC)-Problem zu lösen. Wir haben uns für einen "Mixed Integer Linear Programming" (MILP) Ansatz entschieden, der eine einfache (aber leistungsfähige) Funktion in MATLAB namens **intlinprog()` hat:

[x, fval, exitflag, output] = intlinprog(f, intvars, A, b, Aeq, beq, lb, ub);

Hierbei benutzen wir die folgenden Argumente:

Die mathematische Formel (einschließlich der nicht verwendeten Gleichheitsbeschränkungen \(\textbf{A}_{eq}\) und \(\textbf{b}_{eq}\)), die das Minimierungsprblem beschreibt, sollte dann wie folgt aussehen:

\[ \min_{\textbf{x}}\left(\textbf{f}^{T}\textbf{x}\right)\text{ subject to }\begin{cases}x(i) \in \mathbb{Z}\\\textbf{A}\cdot\textbf{x}\leq\textbf{b}\\\textbf{A}_{eq}\cdot\textbf{x}=\textbf{b}_{eq}\\\textbf{b}_l\leq\textbf{x}\leq\textbf{b}_u\end{cases}\]

Das sieht soweit schön und gut aus, aber... Die Ungleichheitsbeschränkungen \(\textbf{A}\) und \(\textbf{b}\) können sehr groß werden. Die aktuellen Durchschnittsgrößen sind zum Beispiel:

>> size(A)
ans =
    963526 683280

>> size(b)
ans =
    963526 1

Würden diese Matrizen als einfache Arrays mit 8-Bit Ganzzahlen gespeichert, wären mehr als 600 GB Speicher erforderlich. Glücklicherweise können MATLAB's dünnbesetzte Matrizen diese Matrizen relativ einfach handhaben und schließlich das MILP-Problem lösen; aber zu welchem Preis?

CPLEX vs. MATLAB

Die Lösung unseres UC-Problems für einen oder zwei Tage reduziert die Größe der Arrays erheblich. Somit ist eine Lösung innerhalb einer Minute erreicht. Wenn wir jedoch die Anzahl der Tage erhöhen, ist dies der Trend, den wir beobachten:

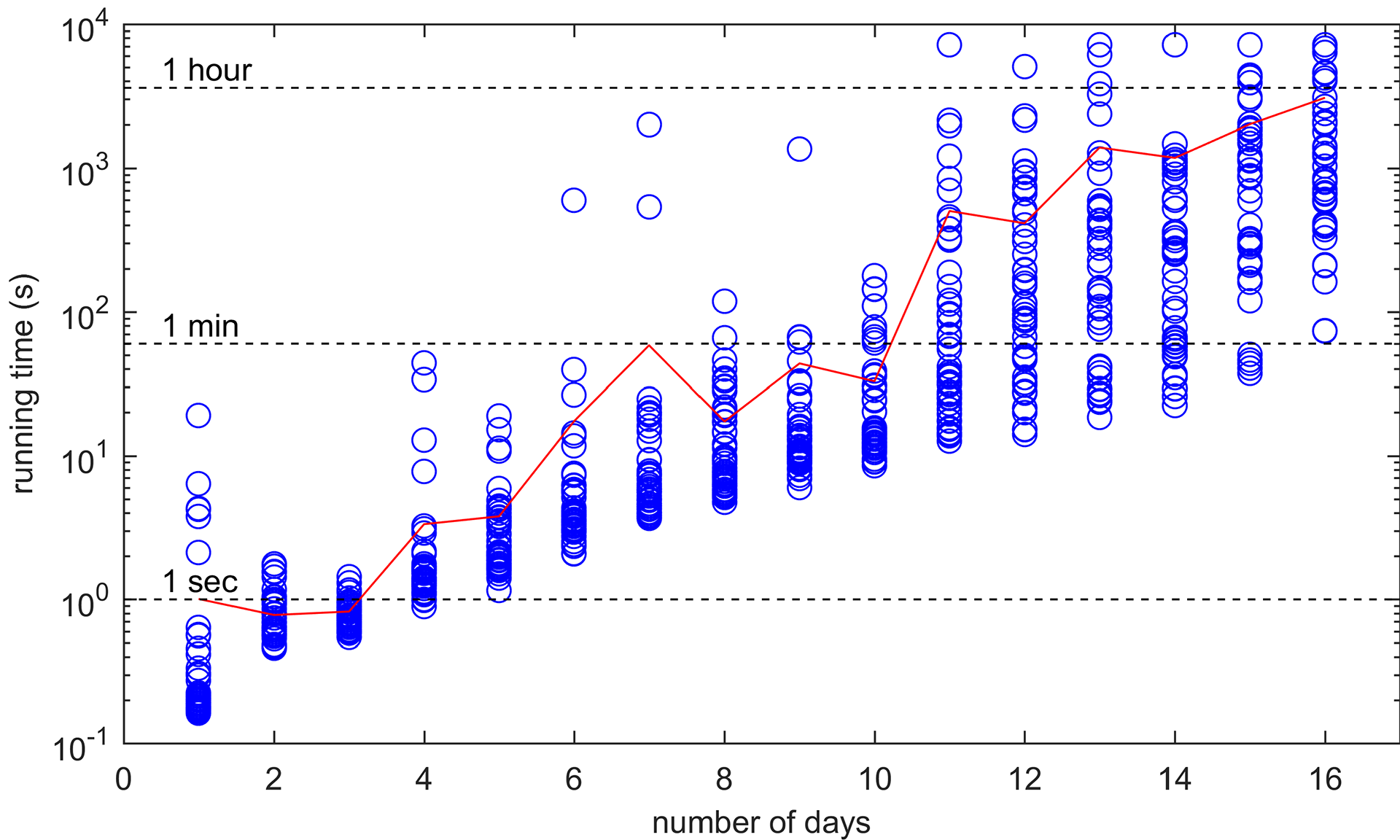
Laufzeit vs. Anzahl der Tage (durchschnittliche Laufzeit in rot)

Man beachte, dass die Y-Achse eine logarithmische Skala hat. Ich habe 50 MILP-Lösungen für verschiedene aufeinanderfolgende Kombinationen von Tagen durchgeführt und die Zeit notiert, die für die Lösung benötigt wurde. Nachdem wir 16 Tage erreicht hatten, dauerte die Lösung so lange, dass es sich nicht mehr gelohnt hat, weiterzumachen. Es sieht so aus, als ob die Zeit, die zum Lösen benötigt wird, exponentiell mit der Anzahl der Tage zunimmt, und auch die Spanne der Rechenzeit wird größer. Wenn sich dieser Trend fortsetzt (und wir vermuten, dass dies der Fall sein wird), wird die Lösung für 365 Tage etwas zwischen 0,63 Tagen und 2800 Jahren dauern (je nachdem, welche Polynomenordnung wir extrapolieren).

Also haben wir IBMs CPLEX Solver installiert und den entsprechenden "Binary Integer Linear Programming" (BILP) Solver ausgeführt. Sein Funktionsaufruf verwendet exakt die gleiche Mathematik und ist daher dem Funktionsaufruf von MATLAB erstaunlich ähnlich:

[x, fval, exitflag, output] = cplexbilp(f, A, b, Aeq, beq, x0, options);

Da die Ausgabe ein binärer Vektor sein sollte, brauchen wir x nicht mit intvars, lb und ub einzuschränken. Man muss jedoch einige Startbedingungen in x0 angeben, aber das kann nur ein einfacher Nullvektor sein. Das Lösen wird nun deutlich beschleunigt:

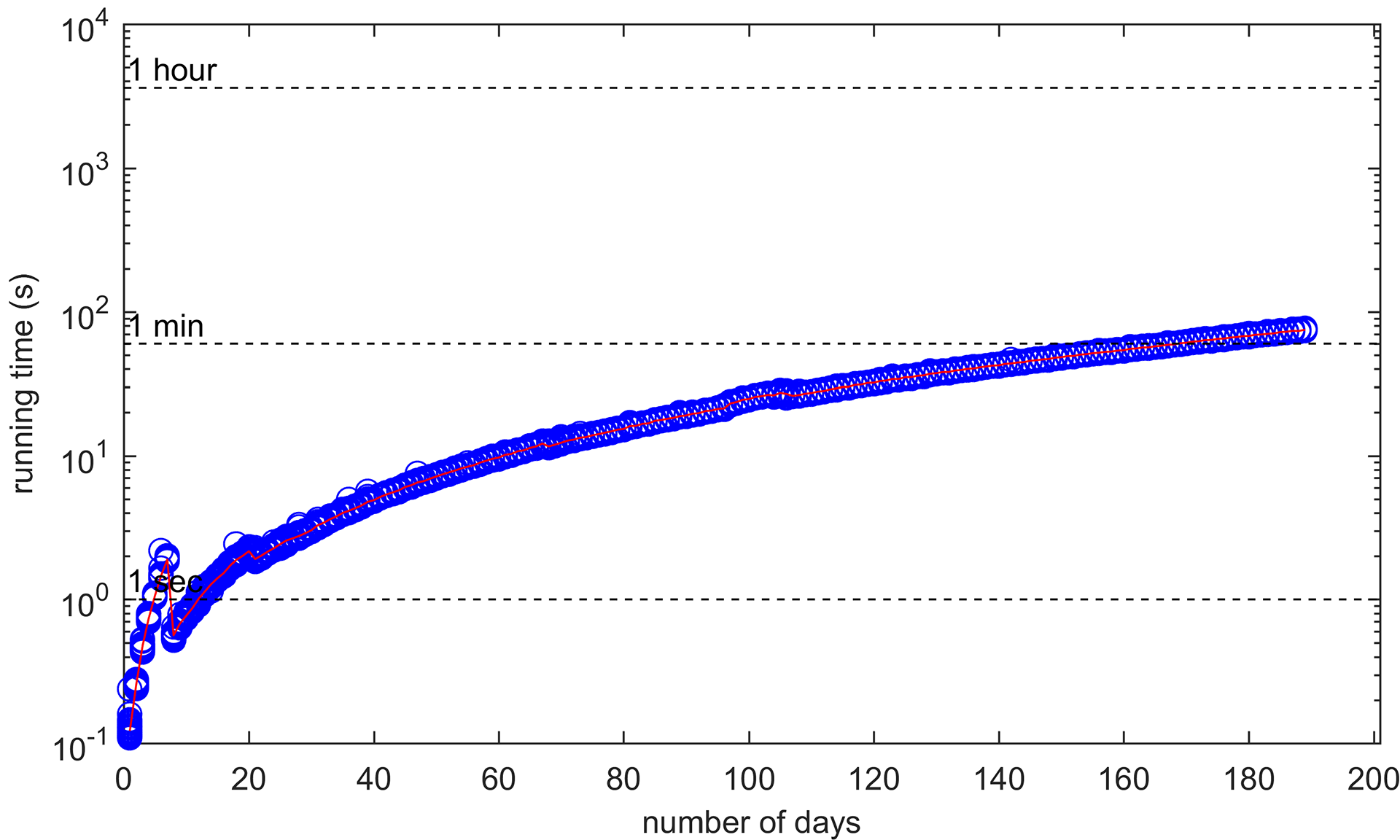
Laufzeit vs. Anzahl der Tage (durchschnittliche Laufzeit in rot)

Ich habe nur mehrere Simulationen bis zu einem halben Jahr durchgeführt, aber man erkennt schon, wie viel schneller und zuverlässiger der IBM-Solver arbeitet. Tatsächlich dauerte die Berechnung der Lösung für ein einzelnes Jahr weniger als 12 Minuten (auf einer virtuellen Maschine auf meinem MacBook Pro). CPLEX ist daher ein erstaunliches, "plug and play" ähnliches Tool, das einfach funktioniert; und es funktioniert wirklich gut!

CPLEX beschaffen

Wie man sich wahrscheinlich denken kann, ist CPLEX erstaunlich. Aber wie bekommt man es und verwendet es in MATLAB? Ganz einfach... Man folge dem Link auf der Website von IBM:

https://www.ibm.com/developerworks/community/blogs/jfp/entry/CPLEX_Is_Free_For_Students

Dann meldet man sich mit einer Studenten-E-Mail-Adresse an, die mit @xxx.edu oder @xxx.ac.uk enden muss, um sicherzustellen, dass man ein Student oder Mitarbeiter an der Universität ist. Nachdem die E-Mail-Adresse bestätigt wurde, kann man den Installer für "IBM ILOG CPLEX Optimization Studio 12.7.1 - Student (CJ1HQML)" kostenlos herunterladen (12.7.1 kann sich je nach aktueller Version ändern). Nun das Setup ausführen und fertig ist die Beschaffung von CPLEX.

In MATLAB muss lediglich die ToolboxCPLEX zum Suchpfad hinzugefügt werden. Dies kann durch diese einfachen Zeile Code erreicht warden:

addpath('C:\Program Files\IBM\ILOG\CPLEX_Studio1271\cplex\matlab\x64_win64');

Man beachte, dass dieser Pfad für verschiedene Versionen von CPLEX unterschiedlich sein kann. Um den richtigen Pfad zur CPLEX Toolbox zu finden, navigiert man einfach zu dem Ordner, in dem CPLEX Studio zuvor installiert wurde. Dort sucht man dann das Verzeichnis matlab und wählt den Ordner der passenden Systemarchitektur (in meinem Fall war es x64_win64) aus. Sobald sichergestellt ist, dass die Funktion addpath(); den richtigen Pfad zu diesem Ordner verwendet, ist alles richtig vorbereitet.

Weitere Informationen findet man auf der IBM-Seite CPLEX für MATLAB (für Version 12.7.1: Link). Nun aber ist meine Mittagspause (in der ich diesen Beitrag geschrieben habe) definitiv vorbei, und ich muss weiter arbeiten. Ich wünsche allen viel Spaß beim Lösen von mathematischen Problemen; vor allem wenn die gerfficiently gelöst werden!