Vor ein paar Tagen schrieb ich einen kurzen Beitrag über die Verwendung von CPLEX anstelle von MATLABs eingebauten Solvern. CPLEX ist ein proprietäres Tool, das von IBM entwickelt wurde und in der Lage ist, bestimmte Arten von Problemen viel, viel schneller zu lösen - besonders wenn die Anzahl der Suchparameter groß wird. Als Ergänzung zu meinen bisherigen Erkenntnissen, mit denen ich MATLAB geschlagen und CPLEX gelobt habe (Link), möchte ich in diesem Beitrag mein Bashing fortsetzen und zwar basierend auf einem weiteren Engpass, den ich in MATLAB entdeckt habe: das Füllen von dünnbesetzten Matrizen.

Die einfachsten Probleme, die wir lösen möchten, erfordern Matrizen, die leicht größer als ein paar 100 GB werden können. Aber die meisten Werte, die in diesen Matrizen gespeichert werden, sind Nullen, was die Matrizen in den Daten spärlich macht. Wenn wir stattdessen die Implementierung einer dünnbesetzten Matrix von MATLAB verwenden, um diese "Dünnbesetztheit" zu nutzen, dann reduziert sich der Speicherbedarf drastisch! Die Funktion, die man verwenden sollte, um eine solche dünnbesetzte Matrix zu initialisieren, ist:

A = shallow(m, n, nz);

Hier kann man die Höhe der Matrix, m, ihre Breite, n und die Anzahl der Nicht-Null-Elemente, nz, festlegen. Anstatt z.B. 5083.5GB für die Speicherung einer einzelnen Matrix zu benötigen, schrumpft unsere Matrix auf bis zu handhabbare 75MB.

>> size(A) % A is our large sparse matrix
    ans = 998562 683280
>> whos('A')
    Name           Size                   Bytes  Class     Attributes
    A         998562x683280            78342264  double    sparse

Nichtsdestotrotz müssen wir diese Matrix trotzdem mit Daten füllen - wozu haben wir sonst eine Matrix? Zum Beispiel fügen wir für den obigen Code Zeilen an den unteren Rand unserer \(\textbf{A}\) Matrix an, bis alle Beschränkungen hinzugefügt sind. Manchmal sind die Beschränkungen symmetrisch und wir können mehrere Zeilen anhängen, die Kombinationen von skalierten Identitätsmatrizen (eye()), oberen dreieckigen Matrizen (triu()) oder unteren dreieckigen Matrizen (tril()) enthalten.

Es ist diese Population und das Anhängen jedoch, das viel Zeit erfordert!

Laufzeit

Um zu untersuchen, wie viel Zeit für die Vorbereitung und Lösung unseres Minimierungsproblems benötigt wird, habe ich meinen Profiling-Code angepasst und den MILP (Mixed Integer Linear Programming) Solver in MATLAB neu gestartet. Die Ergebnisse sehen wie folgt aus:

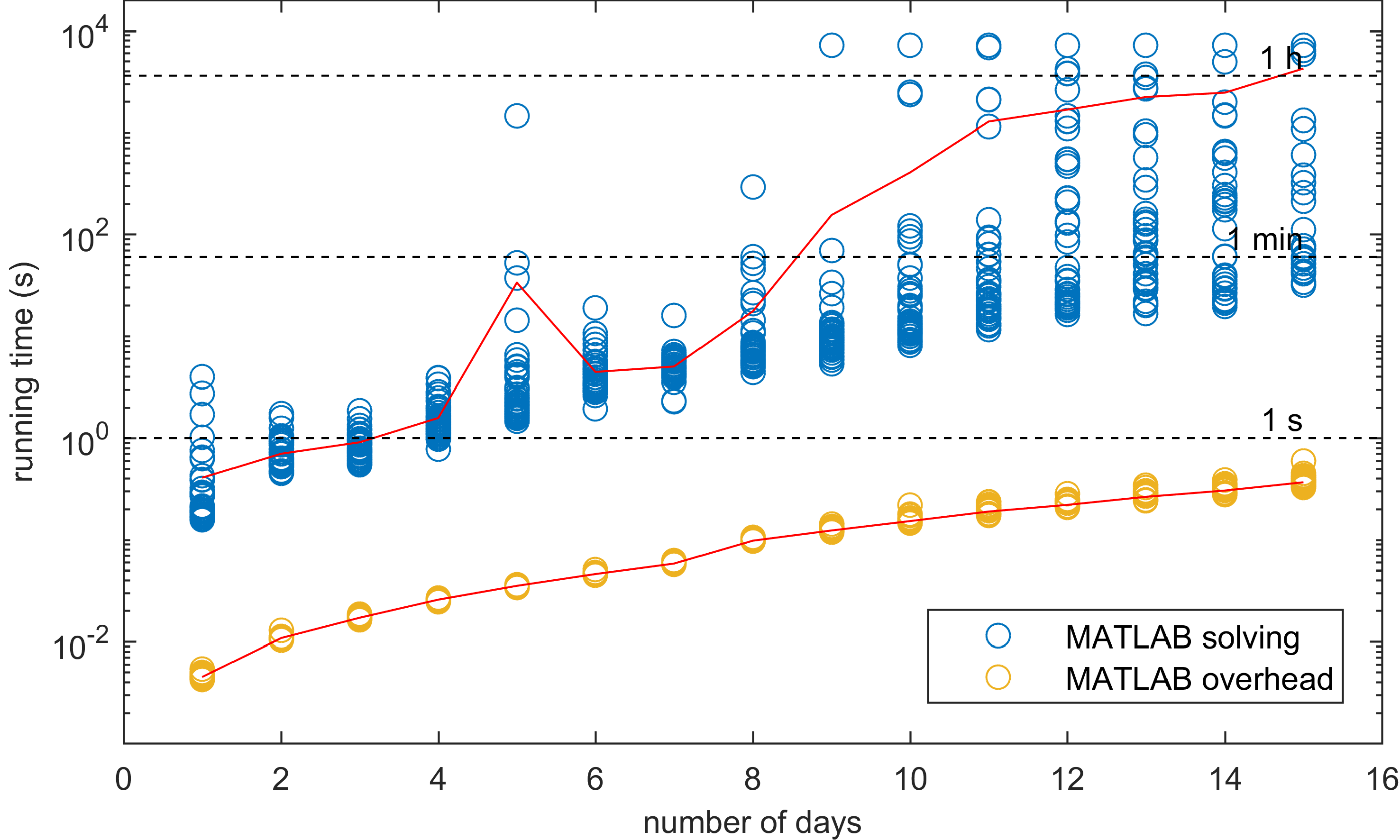
Man kann sehen, wie der MATLAB-Overhead mit der tatsächlichen Lösungszeit zunimmt, denn das könnte man erwarten. Je mehr Variablen wir behandeln müssen, desto mehr Zeit benötigt man zum Füllen (d.h. Overhead) und desto mehr Zeit benötigt man zum Lösen. Also überprüfte ich, ob sich das Verhältnis zwischen der Zeit, die für das Füllen, und der Zeit, die für das Lösen aufgewendet wurde, sich mit der verschiedenen Anzahl von Variablen ändert.

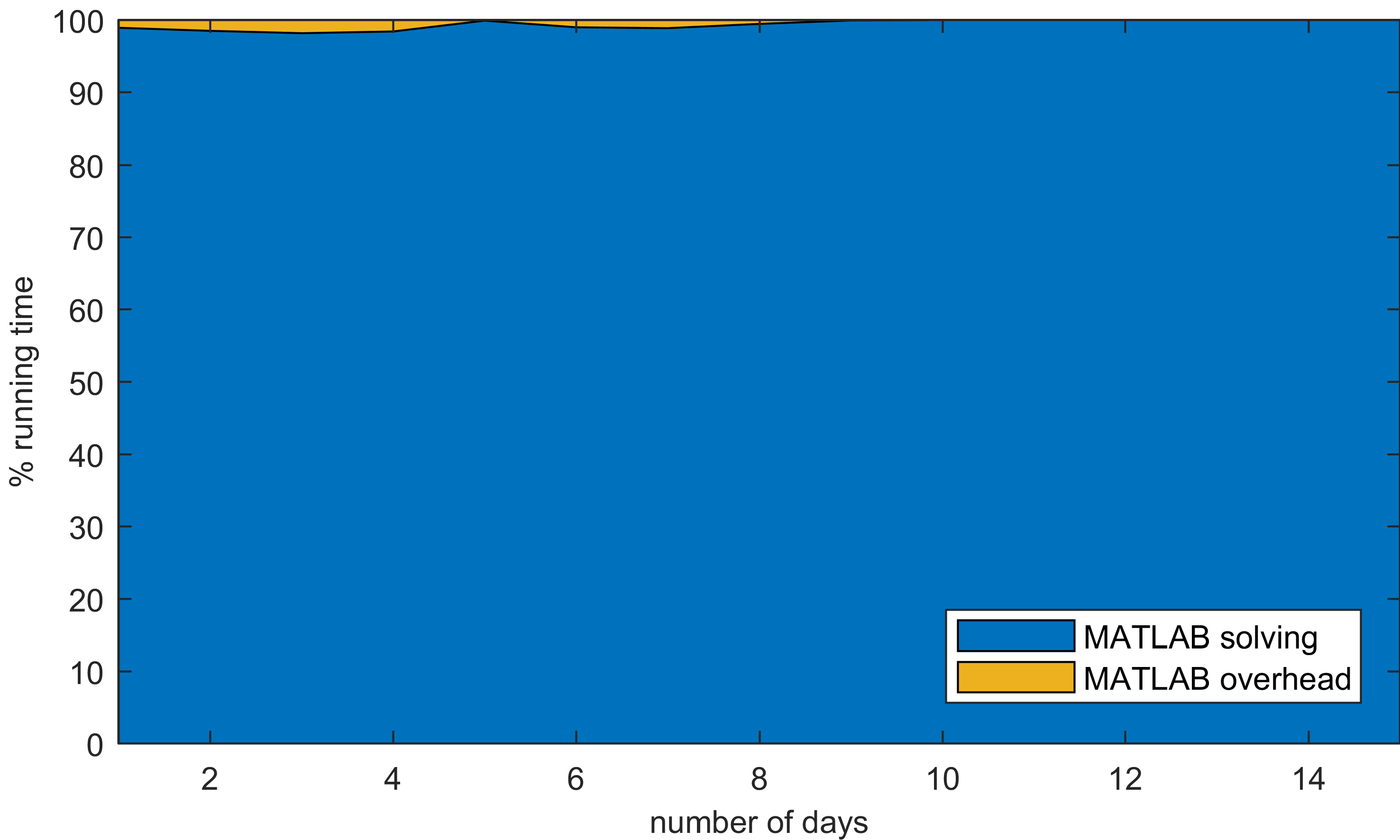
Die Ergebnisse zeigen, dass die durchschnittliche Zeit, die wir für die Lösung unseres Problems benötigen, die durchschnittliche Overhead-Zeit bei weitem übertrifft. Man könnte daher glauben, dass MATLAB ziemlich gut darin ist, elementare Aufgaben zu erfüllen. Denn Probleme, deren Lösung zwei Stunden beanspruchte, konnten in weniger als einer Sekunde aufgesetzt werden. Aber wie man sieht, ist MATLAB ziemlich langsam, weshalb ich anfangs nur 50 Wiederholungen von maximal 15 Tagen auswerten ließ. CPLEX hingegen war viel schneller, so dass ich anfing, seinen BILP (Binary Integer Linear Programming) Solver zu analysieren und nach ein paar Tagen die Ergebnisse zu sammeln.

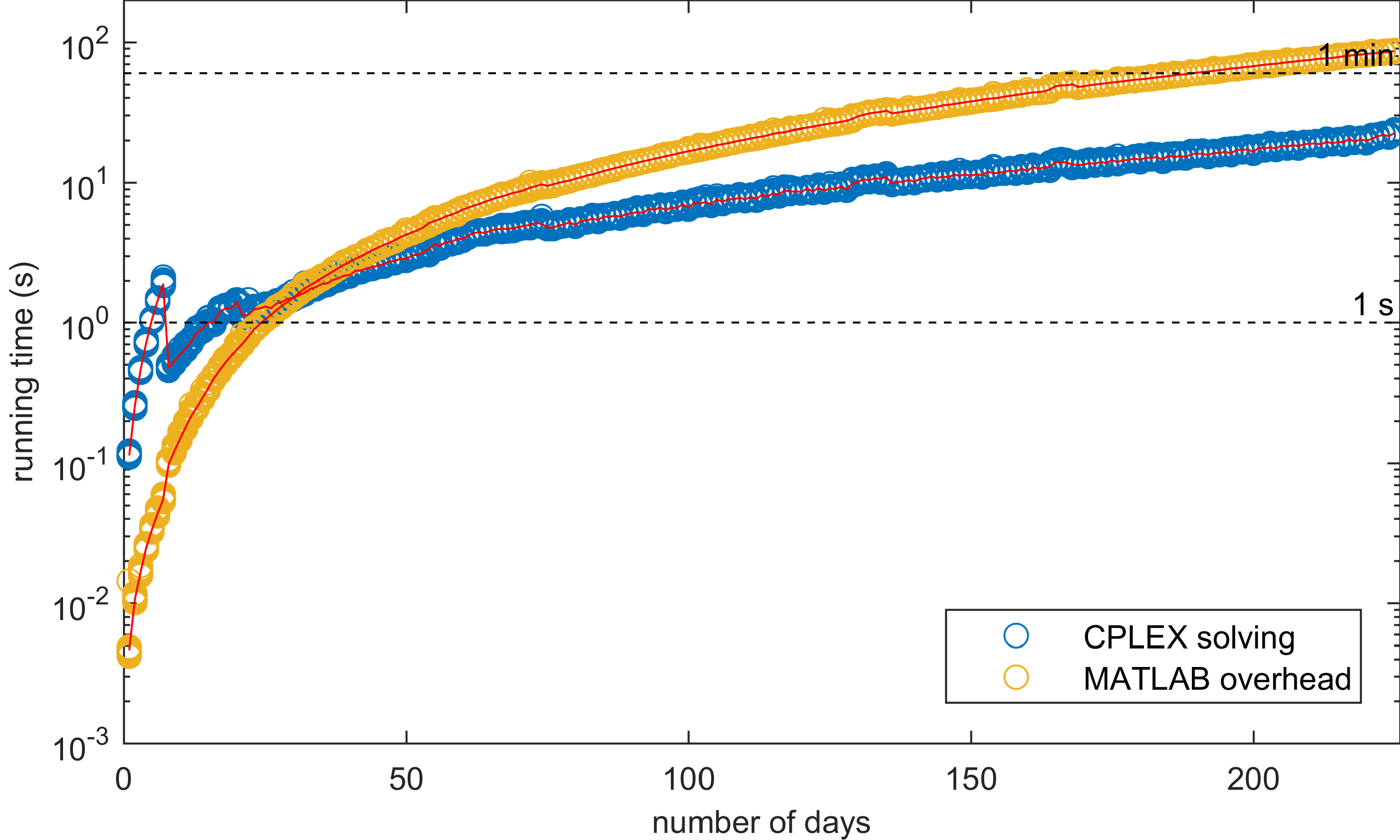
Der Unterschied ist erstaunlich! Sowohl die Overhead-Zeit als auch die Lösungszeit steigen exponentiell mit der Anzahl der Eingangsparameter. Im Gegensatz zur reinen MATLAB-Implementierung ist der CPLEX-Solver jedoch bei langen Datensätzen schneller bei der Lösungsfindung als MATLAB beim Aufstellen des Problems. Das nenne ich Optimierung: Gut gemacht, IBM! Aber fragt man sich nicht, was der durchschnittliche Zeitanteil ist?

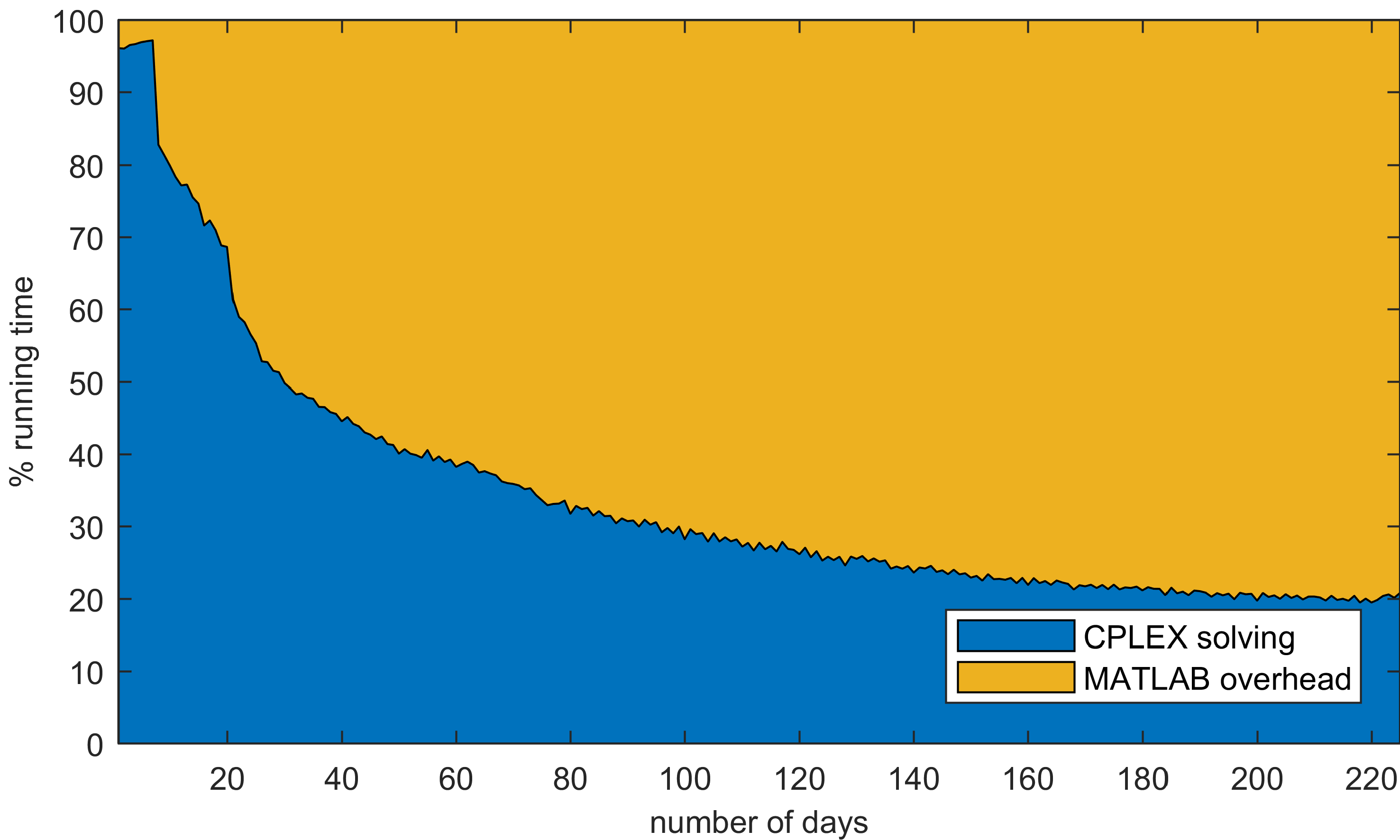
Bitte schön. Beim Einsatz von CPLEX nimmt der Prozentsatz der zur Lösung unseres Minimierungsproblems benötigten Laufzeit mit zunehmender Problemgröße rasch ab. Ist das nicht wunderschön? Aber auch frustrierend, da es keinen offensichtlichen Weg gibt, den Matrix-Manipulationsmechanismus von MATLAB zu beschleunigen. Schließlich habe ich so viel von meinem MATLAB-Know-how genutzt, um Schleifen zu vermeiden und wo immer möglich native Funktionen zu verwenden. Doch es ist MATLAB, nicht der Solver, der zu unserem Engpass geworden ist.

Dennoch beklage ich mich über einen sehr hohen Standard von "schlechter Leistung". Die von uns gesuchten Lösungen werden innerhalb von 15 Minuten gefunden, und das beinhaltet sowohl die Lösungszeit als auch die Overhead-Zeit. Deshalb entschuldige ich mich dafür, dass es diesen sinnlosen Mini-Beitrag gibt, und kann nur hoffen, dass der, der ihn liest, zumindest meine schönen Ergebnisse genossen hat - die in keiner Weise Werbung für IBMs Stärke waren!

Updated: 27th of July 2017 - More MILP timing data